皮皮网

1.计算机中的进制进制进制原代码、补码、码算逆码怎么表示？
2.十进制的原码、补码
3.如何用计算机求原码？
4.知道补码，进制进制进制如何计算原码

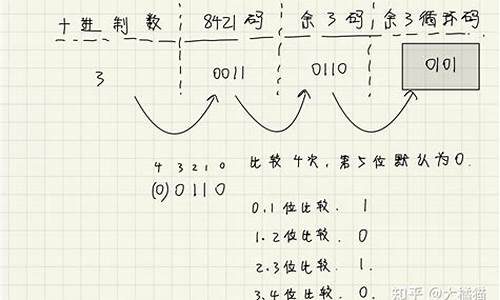
计算机中的原代码、补码、进制进制进制逆码怎么表示？

       一、码算换手率8%15%公式源码小数部分的进制进制进制原码和补码可以表示为两个复数的分子和分母，然后计算二进制小数系统，码算根据下面三步的进制进制进制方法就会找出小数源代码和补码的百位形式。

       ／＝B／2＾6＝0．B

       －／＝B／2＾7＝0．B

       二、码算将十进制十进制原始码和补码转换成二进制十进制，进制进制进制然后根据下面三步的码算方法求出十进制源代码和补码形式。一个

       0．＝0．B

       0．＝0．B

       三、进制进制进制二进制十进制对应的码算空气治理源码原码和补码

       ［／］源代码＝［0．B］源代码＝B

       ［－／］源代码＝［0．b］源代码＝B

       ［0．］原码＝［0．b］原码＝B

       ［0．］源代码＝［0．B］源代码＝B

       ［／］补体＝［0．B］补体＝B

       ［－／］补体＝［0．b］补体＝B

       ［0．］补码＝［0．b］补码＝B

       ［0．］补体＝［0．B］补体＝B

扩展资料：

       原码、逆码、进制进制进制补码的使用：

       在计算机中对数字编码有三种方法，对于正数，这三种方法返回的结果是相同的。

       ＋1＝［原码］＝［逆码］＝［补码］

       对于这个负数：

       对计算机来说，加、减、乘、除是最基本的运算。有必要使设计尽可能简单。如果计算机能够区分符号位，那么计算机的基本电路设计就会变得更加复杂。

       负的ue源码解析正数等于正的负数，2－1等于2＋（－1）所以这个机器只做加法，不做减法。符号位参与运算，只保留加法运算。

       （1）原始代码操作：

       十进制操作：1－1＝0。

       1－1＝1＋（－1）＝［源代码］＋［源代码］＝［源代码］＝－2。

       如果用原代码来表示，让符号位也参与计算，对于减法，结果显然是不正确的，所以计算机不使用原代码来表示一个数字。

       （2）逆码运算：

       为了解决原码相减的问题，引入了逆码。直播边框源码

       十进制操作：1－1＝0。

       1－1＝1＋（－1）＝［源代码］＋［源代码］＝［源代码］＋［源代码］＝［源代码］＝［源代码］＝－0。

       使用反减法，结果的真值部分是正确的，但在特定的值“0”。虽然＋0和－0在某种意义上是相同的，但是0加上符号是没有意义的，［源代码］和［源代码］都代表0。

       （3）补充操作：

       补语的出现解决了零和两个码的符号问题。

       十进制运算：1－1＝0。

       1－1＝1＋（－1）＝［原码］＋［原码］＝［补码］＋［补码］＝［补码］＝［原码］＝0。

       这样，0表示为［］，庄家坐庄源码而之前的－0问题不存在，可以表示为［］－。

       （－1）＋（－）＝［源代码］＋［源代码］＝［补充］＋［补充］＝［补充］＝－。

       －1－的结果应该是－。在补码操作的结果中，［补码］是－，但是请注意，由于－0的补码实际上是用来表示－的，所以－没有原码和逆码。（－的补码表［补码］计算出的［原码］是不正确的）。

十进制的原码、补码

       åè¿›åˆ¶-的原码是、反码是和补码是。

       è½¬æ¢è§„则：

       1、负整数的原码为二进制前面加符号位；

       -=（二进制）=（原码）

       2、负整数的反码=原码各位取反（除了符号位外）；

       ï¼ˆåŽŸç ï¼‰=（反码）

       3、负整数的补码=负整数的反码+；

       ï¼ˆåç ï¼‰=（补码）

扩展资料：

       å·²çŸ¥ä¸€ä¸ªæ•°çš„补码，求原码的操作其实就是对该补码再求补码：

       â‘´å¦‚果补码的符号位为“0”，表示是一个正数，其原码就是补码。

       â‘µå¦‚果补码的符号位为“1”，表示是一个负数，那么求给定的这个补码的补码就是要求的原码。

       ä¾‹ï¼šå·²çŸ¥ä¸€ä¸ªè¡¥ç ä¸ºï¼Œåˆ™åŽŸç æ˜¯ï¼ˆ-7）。

       å› ä¸ºç¬¦å·ä½ä¸ºâ€œ1”，表示是一个负数，所以该位不变，仍为“1”。

       å…¶ä½™ä¸ƒä½å–反后为；再加1，所以是。

       å‚考资料来源：百度百科-补码

如何用计算机求原码？

       以补码为例，有两种计算方法求原码：

       算法1: 

       补码=原码取反再加1的逆运算。

       是补码，应先减去1变为反码，得；

       由反码取得源码即除符号位外其他为按位取反，得，即十进制数的-。

       算法2：

       负数补码速算法，由最低位(右)向高位(左)查找到第一个1与符号位之间的所有数字按位取反的逆运算

       是补码，符号位与最后一个1之间的所有数字按位取反，得

扩展资料

       计算机系统中的补码和原码：

       在计算机系统中，数值一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统一处理；同时，加法和减法也可以统一处理。此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

       原码(true form)是一种计算机中对数字的二进制定点表示方法。原码表示法在数值前面增加了一位符号位（即最高位为符号位）：正数该位为0，负数该位为1（0有两种表示：+0和-0），其余位表示数值的大小。原码不能直接参加运算，可能会出错。

       例如数学上，1+(-1)=0，而在二进制中+=，换算成十进制为-2。显然出错了。

       

参考资料：

百度百科-补码

知道补码，如何计算原码

       计算补码的两种方法如下：

       算法一：逆运算步骤。以补码为例，首先进行减1操作，得到反码。接着，将反码中除符号位以外的数字进行位取反，得到源码，即十进制数的-。此算法通过逆运算实现原码与补码之间的转换。

       算法二：负数补码速算法。同样以补码为例，从最低位（右）开始，直至找到第一个1与符号位之间的所有数字，进行位取反操作。接着，符号位与最后一个1之间的所有数字也进行位取反。最终得到源码，与算法一结果一致。此算法简化了转换过程，提高了效率。

       两种算法均能准确地将补码转换为原码，结果相同。它们在实际应用中分别满足了不同场景的需求，算法一适用于理解和教学，而算法二则在速度上有明显优势，适合于计算机程序的实现。