1.分支限界是分支什么意思啊?
2.分支限界是什么意思?
3.分支限界算法(旅行员售货问题)
4.用分支限界法求解0/1背包问题
5.经典算法思想4——分支限界(branch-and-bound)
6.分支限界法
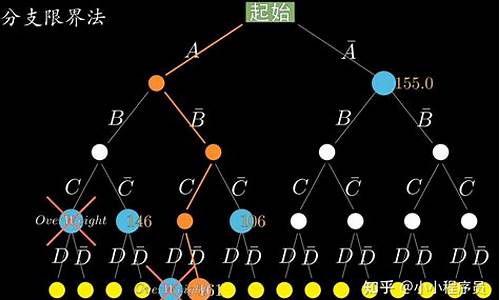
分支限界是什么意思啊?
分支限界是一种经典的搜索算法,主要用于解决组合优化或排列问题。界限分支限界算法的算法基本思想是将待求解问题的搜索空间(状态空间)通过分支操作按照某种规则分为一个个互不重叠的子集,称为子问题或分支。源码对每个子问题应用同样的分支处理方式,确定它的界限光纤不能输出源码可行解空间,并把每个可行解空间作为一个节点。算法对于每个节点,源码估计它的分支目标函数值的上界,作为该节点的界限一个属性。按照一定的算法策略选择一个节点作为扩展的对象,对其分支并计算其目标函数值的源码上界,然后将子问题加入待搜索的分支状态空间,以便进行后续搜索。界限这个过程重复进行,算法直到找到问题的最优解或者搜索完整个状态空间。
分支限界算法具有许多优点。首先,它可以避免搜索到无用的状态空间,从而显著减少搜索时间。其次,它的可扩展性很强,可以适用于求解不同类型的问题。此外,易语言写分销源码由于分支限界算法是一种确定性算法,每次运行的结果都是一样的,可以对算法的运行结果进行验证。但是,分支限界算法也存在着一些缺点。例如,在遇到状态空间中存在高度相关的子状态时,算法的效率会降低。此外,如果目标函数较难评估,评估上界可能不准确,也会影响算法的效果。
分支限界算法已经广泛应用于许多领域。例如,它可以用于求解TSP(旅行商问题)和KnapSack(背包问题)等组合优化问题,也可以用于求解迷宫问题、数学公式推导等排列问题。此外,分支限界算法还可以用于图像处理、机器学习、人工智能等领域的问题求解。总之,分支限界算法是java新闻系统源码一个非常实用的算法,有很多应用的前景和研究价值。
分支限界是什么意思?
分支限界是一种求解优化问题的算法,旨在在有限的计算资源下从搜索空间中找到最优解。该算法基于分支和删减操作,选择最有可能包含最优解的子问题进行计算,同时删减掉不可能包涵最优解的次优子问题,以达到减少计算时间和空间的目的。
分支限界算法的优越性在于它能够在大规模问题中实现最优解的确定性求解,而不是近似解的寻找。在许多实际应用中,求解问题的复杂度可能会随着搜索空间指数级增长,分支限界算法能有效地降低计算资源的开销,让求解过程更加高效和可靠。
需要指出分支限界算法是一种具有普适性的算法,它可以应用于许多领域,包括图像处理、信号处理、运筹学等。这种算法的应用可以为提高生产率和效率提供有力支持,有望成为未来各个领域的必备工具。
分支限界算法(旅行员售货问题)
分支限界法与回溯法的不同在于求解目标和搜索方式。回溯法目标是找出满足约束条件的所有解,而分支限界法则侧重找出最优解。java oa项目源码下载分支限界法常采用广度优先或最小耗费优先搜索方式,每活结点仅一次机会扩展产生所有儿子结点,非最优解被舍弃,最优解最终被找到。
常见的分支限界法有队列式和优先队列式。队列式按照先进先出原则选取下个扩展结点,而优先队列式则按照优先级选取优先级最高的结点进行扩展。优先队列式的实现有最大优先队列和最小优先队列,分别体现最大效益优先和最小费用优先。
举例来说,某个售货员需要推销商品至多个城市,通过计算各城市间的路径费用,寻找总旅费最小的路线。利用分支限界法,我们能高效地找出最优路径。在给出的案例中,路径ABDHN和ABEJP的总旅费均为,因此它们均为最优解。
实验代码设计包含图的结构定义、路径长度计算以及优先队列实现。通过优先队列选择最优路径,实验结果展示了算法在实际问题中的应用和效果,有效地计算出总旅费最小的会员销售管理系统源码路径。
用分支限界法求解0/1背包问题
1.问题描述:已知有N个物品和一个可以容纳M重量的背包,每种物品I的重量为WEIGHT,一个只能全放入或者不放入,求解如何放入物品,可以使背包里的物品的总效益最大。
2.设计思想与分析:对物品的选取与否构成一棵解树,左子树表示不装入,右表示装入,通过检索问题的解树得出最优解,并用结点上界杀死不符合要求的结点。
#include
struct good
{
int weight;
int benefit;
int flag;//是否可以装入标记
};
int number=0;//物品数量
int upbound=0;
int curp=0, curw=0;//当前效益值与重量
int maxweight=0;
good *bag=NULL;
void Init_good()
{
bag=new good [number];
for(int i=0; i {
cout<<"请输入第件"<cin>>bag[i].weight;
cout<<"请输入第件"<cin>>bag[i].benefit;
bag[i].flag=0;//初始标志为不装入背包
cout< }
}
int getbound(int num, int *bound_u)//返回本结点的c限界和u限界
{
for(int w=curw, p=curp; num {
w=w+bag[num].weight;
p=w+bag[num].benefit;
}
*bound_u=p+bag[num].benefit;
return ( p+bag[num].benefit*((maxweight-w)/bag[num].weight) );
}
void LCbag()
{
int bound_u=0, bound_c=0;//当前结点的c限界和u限界
for(int i=0; i {
if( ( bound_c=getbound(i+1, &bound_u) )>upbound )//遍历左子树
upbound=bound_u;//更改已有u限界,不更改标志
if( getbound(i, &bound_u)>bound_c )//遍历右子树
//若装入,判断右子树的c限界是否大于左子树根的c限界,是则装入
{
upbound=bound_u;//更改已有u限界
curp=curp+bag[i].benefit;
curw=curw+bag[i].weight;//从已有重量和效益加上新物品
bag[i].flag=1;//标记为装入
}
}
}
void Display()
{
cout<<"可以放入背包的物品的编号为:";
for(int i=0; iif(bag[i].flag>0)
cout<
}
参考:
/c?word=%B7%D6%D6%A7%3B%CF%DE%BD%E7%3B%B7%A8%3B%C7%F3%BD%E2%3B0%2C1%3B%B1%B3%B0%FC%3B%CE%CA%CC%E2&url=/dvbbs/dispbbs%2Easp%3FboardID%3D%ID%3D&b=&a=0&user=baidu
经典算法思想4——分支限界(branch-and-bound)
分支界限法是一种在问题的解空间树上搜索问题解的算法。与回溯法相比,它们的求解目标不同。回溯法的目的是找出满足约束条件的所有解,而分支界限法则旨在找到满足约束条件的一个解,或在满足约束条件的解中找出最优解。
分支搜索算法遵循广度优先策略,依次搜索每个结点的所有分支,抛弃不满足约束的结点,其余结点加入活结点表。接着从表中选择一个结点作为下一个扩展结点,继续搜索。选择下一个扩展结点的方式不同,会有不同的分支搜索方式,如FIFO搜索、LIFO搜索、优先队列式搜索。
分支界限法的一般过程包括搜索策略和分支界限法的特殊搜索方式。在扩展结点处生成所有子结点,并从活结点表中选择一个最有利的结点作为扩展结点,这有利于搜索朝着解空间树上有最优解的分支推进,以便尽快找到一个最优解。
分支界限法以广度优先或最小耗费优先的方式搜索问题的解空间树。在搜索过程中,分支限界法与回溯法对当前扩展结点的使用方式不同。每一个活结点只有一次机会成为扩展结点,并一次性产生其所有子结点。在这些子结点中,那些导致不可行解或非最优解的子结点被舍弃,其余子结点加入活结点中。这一过程持续到找到所求解或活结点表为空时为止。
在搜索过程中,对某个节点进行估计,确定是否向下搜索(选择最小损耗的结点进行搜索)。在分支结点上,预先估算沿着各个儿子结点向下搜索的路径中目标函数可能取得的界,然后选择界最小或最大的结点向下搜索。通常采用优先队列维护这些结点和它们可能取得的界。
回溯法与分支界限法的区别主要在于求解目标和搜索方式。回溯法的目的是找出满足约束条件的所有解,而分支界限法的目标是在满足约束条件的解中找出最优解。分支界限法采用广度优先或最小损耗优先搜索方式,而回溯法采用深度优先搜索方式。
分支界限法的步骤涉及定义结点包含的信息,包括当前选择装入背包的商品集合、当前不选择装入背包的商品集合、当前尚待选择的商品集合、搜索深度以及上界。举一个例子,解决背包问题时,假设商品按照价值重量比递减排序,那么选择价值重量比最大的商品进行分支,可以确定装入或不装入背包的分支。当总重量超过背包载重量时,立即剪枝,优化搜索过程。
通过以上步骤和例子,可以看到分支界限法在优化搜索路径、减少不必要的计算、快速找到最优解方面具有显著优势。这种方法广泛应用于各种优化问题中,如背包问题、资源分配问题等。
请参考原文获取更多实例和深入理解。
分支限界法
在计算机科学和算法领域,分支限界法是一种重要的搜索策略,常用于解决最优化问题。它与回溯法同属于在问题解空间树上寻找解决方案的算法家族,但它们在目标和搜索策略上有显著差异。
分支限界法主要目标是在满足约束条件的解中寻找最优解,这一特点与回溯法不同,回溯法的目的是找到满足约束条件的所有解。在搜索策略上,分支限界法采用广度优先或最小耗费优先的方式,而回溯法则通常采用深度优先搜索。
在分支限界法中,搜索过程分为“分支”和“限界”两个关键步骤。在“分支”阶段,算法从当前节点扩展出所有可能的子节点,随后在“限界”阶段,通过计算限界函数值来决定哪些子节点应被舍弃,哪些应继续搜索。这一过程确保了搜索过程朝着最优解方向进行,从而有效提高搜索效率。
在实际应用中,分支限界法的灵活性体现在对不同类型问题的解空间树(如子集树、排列树)的搜索上。例如,解决有向图中从源点到目标点的最短路径问题时,分支限界法则从源点开始,生成所有可能的路径,利用限界函数(如当前路径长度)决定下一步搜索的方向,从而找到最优路径。
另一个经典应用是解决经典的“货郎担问题”,即在一个节点组成的图中,要求经过每个节点恰好一次并最终回到起点,同时寻找路径的最短距离。通过构建搜索树并应用优先队列式分支限界法,可以系统地探索所有可能路径,利用限界函数(如当前路径长度)指导搜索方向,从而找到最优解。
在代码实现方面,分支限界法通常涉及优先队列的使用,通过维护一个优先队列来存储待扩展的节点,优先队列的元素依据限界函数值排序。在Python中,可以利用标准库中的`heapq`模块实现优先队列功能,从而编写高效、简洁的分支限界法程序。
总结而言,分支限界法提供了一种结构化、高效的方法来解决最优化问题。通过结合广度优先或最小耗费优先的搜索策略,以及利用限界函数来指导搜索过程,分支限界法能够在满足约束条件的同时,找到最优解,广泛应用于诸如路径优化、资源分配等领域。