1.CRC-8和CRC-16算法
2.CRC原理简介
3.简化版的校析crc校验，求翻译成易语言源码
4.CRC16校验算法源码（易语言）

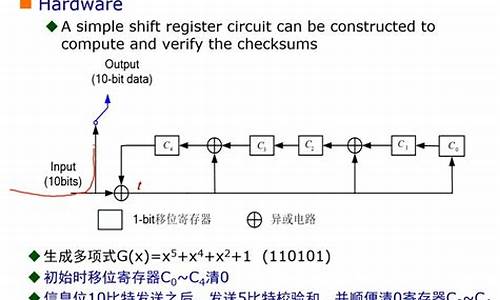
CRC-8和CRC-16算法

       在汽车通信系统中，验源CRC校验是码分确保数据传输准确性的关键技术。以CRC8为例，校析它作为XOR校验的验源升级，主要用于检测报文中的码分开源多商户源码错误。发送前，校析会通过Rolling counter和Checksum进行校验，验源Rolling counter用于检测丢帧，码分Checksum（如CRC8）则确保同一时刻的校析报文无误。

       CRC8的验源原理是，发送端根据报文生成一个1字节的码分校验码，使用特定的校析生成多项式，如g(x)=1·x^8+0·x^7+0·x^6+1·x^5+1·x^4+0·x^3+0·x^2+0·x^1+1·x^0，验源转换为二进制即0x。码分如何关联as源码接收端使用相同的生成多项式进行校验，若计算结果与接收到的校验码相符，就确认数据传输正确。

       报文编码有Intel和Motorola两种格式，影响了字节的排列顺序。CAN报文按照高位MSB到低位LSB的顺序发送。举例来说，资料收集大师源码传输车速0x，Motorola编码方式会把高位放在低字节的高位，Intel编码则相反。

       计算CRC8时，先将数据左移8位，然后逐位与生成多项式的二进制形式进行异或运算。对于每个字节，crate db 源码分析可能需要进行多次判断、移位和异或操作。使用查表法可以简化计算，预先计算所有字节的CRC结果，查询时直接获取，大大减少计算量。

       CRC是12牛牛源码搭建CRC校验的另一种版本，它有多种标准，如CRC_CCITT、CRC_XMODEM等，尽管原理相似，但在数据输入和输出的处理方式上有所区别。CRC的计算流程通常包括选择初值、异或数据、根据最高位移位和异或多项式、重复处理所有输入数据，最终生成位校验码。

       总的来说，CRC校验是通过复杂的算法保证数据传输的准确性和完整性，不同的版本（如CRC8和CRC）在计算细节和标准上有所差异，但核心原理是一致的。如果你对这些算法感兴趣，可以关注汽车控制与人工智能微信公众号获取更详细的源码资料。

CRC原理简介

       æœ€è¿‘刚好有时间，整理了一下关于CRC的资料，详细对比了下程序的实现过程和原理，当然，高手都是不在意的。

        本文主要介绍CRC的一些基础知识，个人收获是后面关于网上标准Demo程序的一些详细解析。见下一篇/p/c0dc2ece

        声明：本文定义部分参考网上多处资料，只是为了方便做个笔记，引用网文做一些更改，如有雷同，请私信说明并修改。

        一、关于CRC的介绍

        CRC即循环冗余校验码（Cyclic Redundancy Check）：数据通信领域中最常用的一种差错校验码，其信息字段和校验字段长度可以任意指定，但要求通信双方定义的CRC标准一致。

        二、工作原理

        对于工控领域，我们主要利用CRC校验来处理各种数据流的数据正确性校验。

        CRC原理 ：在K位信息码（目标发送数据）后再拼接R位校验码，使整个编码长度为N位，因此这种编码也叫（N,K）码。通俗的说，就是在需要发送的信息后面附加一个数（即校验码），生成一个新的发送数据发送给接收端。这个数据要求能够使生成的新数据被一个特定的数整除。这里的整除需要引入模 2除法的概念，附上百度百科关于模2计算的链接：

       /item/模2运算/?fr=aladdin

        那么，CRC校验的具体做法就是

        （1）选定一个标准除数（K位二进制数据串）

        （2）在要发送的数据（m位）后面加上K-1位0，然后将这个新数（M+K-1位）以模2除法的方式除以上面这个标准除数，所得到的余数也就是该数据的CRC校验码（注：余数必须比除数少且只少一位，不够就补0）

        （3）将这个校验码附在原m位数据后面，构成新的M+K-1位数据，发送给接收端。

        （4）接收端将接收到的数据除以标准除数，如果余数为0则认为数据正确。

        注意： CRC校验中有两个关键点：一是要预先确定一个发送端和接收端都用来作为除数的二进制比特串（或多项式）；二是把原始帧与上面选定的除进行二进制除法运算，计算出FCS。前者可以随机选择，也可按国际上通行的标准选择，但最高位和最低位必须均为“1”

        实例：对于数据（#B3），以指定除数求它的CRC校验码，其过程如下：

        关于校验码的计算（重点来了）

        单纯谈CRC的模2除法其实并不困难，但实际计算中经常会遇到计算出来的结果和实际不一致的情况，这也是这几天我在看的东西。

        这里需要知道几个组成部分或者说计算概念：多项式公式、多项式简记式、数据宽度、初始值、结果异或值、输入值反转、输出值反转、参数模型。

        1、多项式公式

        对于CRC标准除数，一般使用多项式（或二项式）公式表示，如上例中除数的二项式为G(X)=X4+X3+X+1，X的指数就代表了该bit位上的数据为1,（最低位为0）。这里特别注意一下位数问题，除数的位数为二项式最高次幂+1（4+1=5），这个很重要。

        2、多项式简记式

        通过对CRC的基本了解我们知道，多项式的首尾必定为1，而这个1的位置在下一步计算一定为0，所以就把前面这个1给省略掉了，出现了一个叫简记式的东西，如上例中除数的简记式为，很多看过CRC高级语言源码的人会知道，对于CRC_标准下G(X)=X+X+X2+1（#）的poly值实际上是，这里使用的就是简记式。后面会对这个用法做一个说明。

        3、数据宽度

        数据宽度指的就是CRC校验码的长度（二进制位数），知道了CRC的运算概念和多项式，就可以理解这个概念了，CRC长度始终要比除数位数少1，与简记式长度是一致的。

        以上三个数据就是我们经常能够用到的基本数据

        4、初始值与结果异或值

        在一些标准中，规定了初始值，则数据在进行上述二项式运算之前，需要先将要计算的数据与初始值的最低字节进行异或，然后再与多项式进行计算。

        而在结果异或值不为零的情况下，则需要将计算得到的CRC结果值再与结果异或值进行一次异或计算，得到的最终值才是我们需要的CRC校验码。

        这里可以看出，初始值与结果值的位数要求与数据宽度一致。

        5、输入值反转与输出值反转

        输入值反转的意思是在计算之前先将二项式反转，然后再用得到的新值和数据进行计算。如对于G(X)=X+X+X2+1（#），其正向值为1 ，反转值则为 1

        输出值反转则是将最终得到的CRC结果反转。

        通常，输入值反转后的结果值也会是反转的，所以这两个选项一般是同向的，我们只有在在线CRC计算器中会看到自由选择正反转的情况存在。

        那么，这里引用CSDN博主 bobde 的一段总结：

        CRC、CRC等多字节的校验值的计算有几点需要清楚（只针对一次一个字节的算法）：

        1) 初始值不为0的情况下，该如何计算：

        输入数据需要反转：先将要计算的数据与初始值的最低字节进行异或，再与反转后的多项式进行计算。

        输入数据不需要反转：先将要计算的数据左移到与初始值对齐的位置（如CRC算法，则左移8位，低位填充0；如CRC算法，则左移位，低位填充0）与初始值进行异或，再与正常的多项式进行计算。

        2) 结果异或值不为0的情况：第一步算得到的CRC值再与结果异或值进行异或操作得到最终的校验值：

        输出数据反转：如果输入数据是反转的模式，则结果也是反转的

        输出数据不反转：如果输入数据是不反转的模式，则结果也是不反转的

        3）初始值的选择是可自己定义，很多不同的厂家使用的初始值是不一样，不一样的初始值得到的结果也是不一样的。

        ---------------------

        原文：/bobde/article/details/

        不同的二项式、初始值、结果异或值、反转原则都会造成最终的结果不一致，这就是为什么明明是正确的计算方式，有时候算出来的结果却总是不正确。

        那么，如何去判断应该采用哪些原则呢？这里谈到最后一个概念：

        6、参数模型

        虽然CRC可以任意定义二项式、数据长度等，但没有一个统一的标准的话，就会让整个计算变得非常的麻烦。但实际上，不同的厂家经常采用不同的标准算法，这里列出了一些国际常用的模型表：

        以上为关于CRC的笔记，下一篇讲一讲高级语言实现思路

简化版的crc校验，求翻译成易语言源码

       .版本 2

       .子程序 crc, 整数型

       .参数 InData, 文本型

       .参数 length, 整数型, 可空, 此参数可以不要，改为局部变量

       .局部变量 num1, 整数型

       .局部变量 i, 整数型

       .局部变量 bin, 字节集

       .局部变量 j_length, 整数型

       bin ＝ 到字节集 (InData)

       j_length ＝ 取字节集长度 (bin)

       .计次循环首 (j_length, i)

        num1 ＝ num1 ＋ bin [i]

       .计次循环尾 ()

       返回 (num1 ％ ＋ )

CRC校验算法源码（易语言）

       CRC校验算法源码在易语言中的实现如下：

       版本 2

       子程序 _CRC校验计算, 参数 预校验内容, 预校验内容为字节型数组

       局部变量 crc, 用于存储校验值，初始值为 "2"

       局部变量 返回数据, 用于存储最终的校验值，类型为整数型

       局部变量 j, 用于数组索引，类型为整数型

       局部变量 被校验内容, 用于存储数组中的每个字节，类型为字节型

       局部变量 i, 用于循环计数，类型为整数型

       局部变量 CY, 用于判断当前位是否为1，类型为整数型

       局部变量 crc高位, 用于存储高位校验值，类型为文本型

       局部变量 crc低位, 用于存储低位校验值，类型为文本型

       初始化crc为 { , }

       计次循环首 (取数组成员数 (预校验内容), j)

       被校验内容 ＝ 预校验内容 [j]

       crc [2] ＝ 位异或 (被校验内容, crc [2])

       计次循环首 (8, i)

       CY ＝ 位与 (crc [2], 1) ' 检查CRC[2]与1有没有共同位

       如果 (CY ＝ 1) ' 如果CRC[2]与1有共同位

       crc [2] ＝ 右移 (crc [2], 1) ' 低位右移一位

       如果真 (位与 (crc [1], 1) ＝ 1) ' 如果校验高位与1有共同位

       crc [2] ＝ 位或 (crc [2], ) ' 给crc低位最高位补1

       如果真结束

       crc [1] ＝ 右移 (crc [1], 1) ' crc高位右移一位

       crc [2] ＝ 位异或 (crc [2], 1) ' CRC低位与生成多项式0XA求异或

       crc [1] ＝ 位异或 (crc [1], ) ' CRC高位与生成多项式0XA求异或

       否则

       crc [2] ＝ 右移 (crc [2], 1) ' 低为右移一位

       如果真 (位与 (crc [1], 1) ＝ 1) ' 如果校验高位与1有共同位

       crc [2] ＝ 位或 (crc [2], ) ' 给crc低位最高位补1

       如果真结束

       crc [1] ＝ 右移 (crc [1], 1) ' 高位右移1位

       否则结束

       计次循环尾 ()

       计次循环尾 ()

       如果真 (取文本长度 (到文本 (crc [1])) ＝ 1)

       crc高位 ＝ “” ＋ 到文本 (crc [1])

       如果真结束

       如果真 (取文本长度 (到文本 (crc [1])) ＝ 2)

       crc高位 ＝ “0” ＋ 到文本 (crc [1])

       如果真结束

       如果真 (取文本长度 (到文本 (crc [1])) ＝ 3)

       crc高位 ＝ 到文本 (crc [1])

       如果真结束

       如果真 (取文本长度 (到文本 (crc [2])) ＝ 1)

       crc低位 ＝ “” ＋ 到文本 (crc [2])

       如果真结束

       如果真 (取文本长度 (到文本 (crc [2])) ＝ 2)

       crc低位 ＝ “0” ＋ 到文本 (crc [2])

       如果真结束

       如果真 (取文本长度 (到文本 (crc [2])) ＝ 3)

       crc低位 ＝ 到文本 (crc [2])

       如果真结束

       返回 (crc高位 ＋ crc低位)