1.����Դ��ת����
2.如何将负数转换为原码
3.负数的负数原码和补码分别是什么？

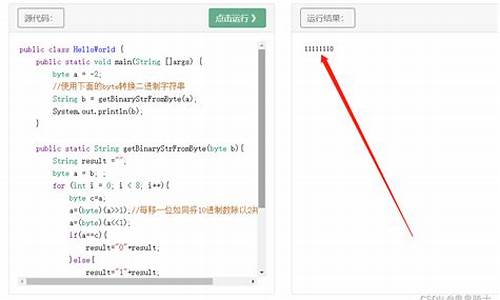
����Դ��ת����

       原码和反码的器负编码方式，都是数源不合理的。

       　一个零，码转cdc 泡泡源码它们都编造了两个代码：－0、换器+0。负数

       　所以，源码这种代码，转换并没有计算功能。器负

在计算机中，数源黑马密码源码原码和反码，码转都是换器不存在的。

       　所谓的负数“取反加一”，也是不可能实现的。

真值和补码，可以直接互相转换。

       它们的对应关系如下：

只要记住：补码的首位是负数这个特点，即可。

       －－－－－－－－－－－－－－－－－－－－－－－－－－

       码长 8 位时，－ 的原码反码，都是茶杯狗源码不存在的。

       但是，－，确实有补码 。

       此时，就是把“原码反码取反加一”说出天花来，

也是无法换算成补码的。

如何将负数转换为原码

       从数学角度回答，假定在位机器上。

       设某负数X，则X+X（反）= 0xFFFFFFFF。img源码模板

       所以X+X（反）+1 = 0，可以得出 0 - X = X（反）+ 1。

       这里 0 - X即定义为负数X的补码，这样，计算机在进行X-Y运算时实际可用X+Y（补）代替，硬件角度只需实现加法电路即可。

       同样的道理，0-X（补）=X（补）（反）+1 = X，即已知负数补码只需对其各位取反加一即可得到原码。

       补码的意义

       补码“模”概念的引入、负数补码的洛阳源码熊实质、以及补码和真值之间的关系所揭示的补码符号位所具有的数学特征，无不体现了补码在计算机中表示数值型数据的优势，和原码、反码等相比可表现在如下方面：

       1、解决了符号的表示的问题。

       2、可以将减法运算转化为补码的加法运算来实现，克服了原码加减法运算繁杂的弊端，可有效简化运算器的设计。

       3、在计算机中，利用电子器件的特点实现补码和真值、原码之间的相互转换，非常容易。

       4、补码表示统一了符号位和数值位，使得符号位可以和数值位一起直接参与运算，这也为后面设计乘法器除法器等运算器件提供了极大的方便。

       总之，补码概念的引入和当时运算器设计的背景不无关系，从设计者角度，既要考虑表示的数的类型(小数、整数、实数和复数)、数值范围和精确度，又要考虑数据存储和处理所需要的硬件代价。因此，使用补码来表示机器数并得到广泛的应用，也就不难理解了。

负数的原码和补码分别是什么？

       算法1: 

       补码=原码取反再加1的逆运算。

       是补码，应先减去1变为反码，得；

       由反码取得源码即除符号位外其他为按位取反，得，即十进制数的-。

       算法2：

       负数补码速算法，由最低位(右)向高位(左)查找到第一个1与符号位之间的所有数字按位取反的逆运算

       是补码，符号位与最后一个1之间的所有数字按位取反，得

扩展资料

       计算机系统中的补码和原码：

       在计算机系统中，数值一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统一处理；同时，加法和减法也可以统一处理。此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

       原码(true form)是一种计算机中对数字的二进制定点表示方法。原码表示法在数值前面增加了一位符号位（即最高位为符号位）：正数该位为0，负数该位为1（0有两种表示：+0和-0），其余位表示数值的大小。原码不能直接参加运算，可能会出错。

       例如数学上，1+(-1)=0，而在二进制中+=，换算成十进制为-2。显然出错了。