1.让你久等了!《码出高效:Java 开发手册》正式发布
2.Timsort详解
3.第一天:Arrays.sort和Collection实现原理
4.TimSort: C/C++版本
让你久等了!《码出高效:Java 开发手册》正式发布
欢迎Java开发者,让我们共同期待的《码出高效:Java 开发手册》正式发布了!9月日,杭州云栖大会见证了这一重要时刻,贴吧 云 源码同时,此书宣布将所有图书收益捐赠至公益项目,献出一份爱心。历时两年精心打磨,这本书承载着制作团队对优质内容的追求,旨在为中国计算机领域树立标杆。
《码出高效:Java 开发手册》源自《阿里巴巴Java开发手册》,一经公布即引起广泛讨论,影响全球数百万开发者,甚至远播硅谷。其配套的扫描插件使万开发者下载,数千家企业内部采用。手册在研发效能、域名注册查询源码人才培养与系统稳定性方面产生深远影响,成为开发基础标准文件。
为满足更多开发者对《手册》深入理解的需求,此书应运而生。它以轻松的文风,结合阿里巴巴实践,与底层源码解析相辅相成,旨在提升Java开发者实力。知识内容丰富,涵盖计算机基础知识、面向对象理念、JVM核心解析、数据结构与集合、高并发多线程、异常与日志、单元测试以及优雅代码编写,由浅入深,满足不同阶段开发者需求。wap商城源码下载
本书不仅提供理论知识,还通过搜集线上真实故障进行案例讲解,帮助开发者理解故障背后的逻辑,增强实战能力。同时,紧跟业界前沿,解析JDK源码及相关特性,如var关键字使用、函数式表达式、红黑树、TimSort等,确保内容与技术发展同步。
从团队协作角度出发,本书旨在提升沟通与协作效率,使开发者在追求个性与美感的同时,实现高效协同。书中内容不仅适用于团队,也适用于个人成长。快递批量查询源码从初级入门到高级修炼,本书为每位开发者提供成长路径。
此外,此书采用彩色印刷,确保最佳阅读体验。目前,该书已开放购买,通过指定链接,即可获取受益一生的编码习惯,了解技术背后的原理。复制下方口令,打开天猫或淘宝App,即可购买。
复制整段信息,打开天猫APP:码出高效 Java开发手册 杨冠宝 高海慧 Java开发核心技术 Java程序开发教程 Java工程师入职指南Java后端技能点参考手册Java工程师(未安装App点这里: zmnxbc.com/s/V1mjU?...) 喵口令
Timsort详解
TimSortæ¯ç»åäºå并æåºï¼å并æåºï¼åæå ¥æåºï¼æå ¥æåºï¼èå¾åºçæåºç®æ³ï¼å®å¨ç°å®ä¸æå¾å¥½çæç.Tim Peterså¨å¹´è®¾è®¡äºè¯¥ç®æ³å¹¶å¨Pythonä¸ä½¿ç¨æ¯Pythonä¸list.sortçé»è®¤å®ç°ï¼ã该ç®æ³æ¾å°æ°æ®ä¸å·²ç»æ好åºçå - ååºï¼æ¯ä¸ä¸ªååºå«ä¸ä¸ªrunï¼ç¶åæè§åå并è¿äºrun.Pyhtonèªä»2.3çæ¬ä»¥åä¸ç´éç¨Timsortç®æ³æåºï¼ç°å¨Java SE7åAndroidä¹éç¨Timsortç®æ³å¯¹æ°ç»æåºãå 容
1æä½
2æ§è½
3JDKæºç
Timsortæ ¸å¿çè¿ç¨
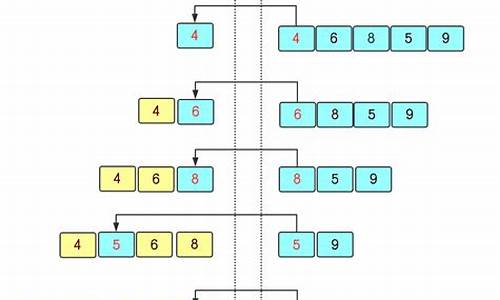
TimSortç®æ³ä¸ºäºåå°å¯¹ååºé¨åçåé¦å对éåºé¨åçæ§è½åéï¼å°è¾å ¥æå ¶ååºåéåºç¹ç¹è¿è¡äºååºãæ¯æ¬¡å并ä¼å°ä¸¤ä¸ªè¿è¡å并æä¸ä¸ªè¿è¡ãå并çç»æä¿åå°æ ä¸ãå并ç´å°æ¶èæææçè¿è¡ï¼è¿æ¶å°æ ä¸å©ä½çè·å并å°åªå©ä¸ä¸ªè·ä¸ºæ¢ãè¿æ¶è¿ä¸ªä» å©çè·ä¾¿æ¯æ好åºçç»æã
综ä¸è¿°è¿ç¨ï¼Timsortç®æ³çè¿ç¨å æ¬
ï¼0ï¼å¦ä½æ°ç»é¿åº¦å°äºæ个å¼ï¼ç´æ¥ç¨äºåæå ¥æåºç®æ³
ï¼1ï¼æ¾å°å个è¿è¡ï¼å¹¶å ¥æ
ï¼2ï¼æè§åå并è¿è¡
1æä½
ç°å®ä¸ç大å¤æ°æ®é常æ¯æé¨åå·²ç»æ好åºçï¼Timsortå©ç¨äºè¿ä¸ç¹ç¹.Timsortæåºçè¾å ¥çåä½ä¸æ¯ä¸ä¸ªä¸ªåç¬çæ°åï¼èæ¯ä¸ä¸ªä¸ªçååºãå ¶ä¸æ¯ä¸ä¸ªååºå«ä¸ä¸ªâè¿è¡âï¼å¾1ï¼ãé对è¿ä¸ªrunåºåï¼æ¯æ¬¡æ¿ä¸ä¸ªrunåºæ¥è¿è¡å½å¹¶ãæ¯æ¬¡å½å¹¶ä¼å°ä¸¤ä¸ªrunå并æä¸ä¸ªrunãæ¯ä¸ªrunæå°è¦æ2个å ç´ .Timesoræç §ååºåéåºåååºæ¯ä¸ªrunï¼runå¦ææ¯æ¯ååºçï¼é£ä¹è¿è¡ä¸çåä¸å ç´ è¦å¤§äºæçäºåä¸å ç´ ï¼a [lo] <= a [lo + 1] <= a [lo + 2] <= ... ï¼;å¦ærunæ¯ä¸¥æ ¼éåºçï¼å³è¿è¡ä¸çåä¸å ç´ å¤§äºåä¸å ç´ ï¼a [lo]> a [lo + 1]> a [lo + 2]> ...ï¼ï¼éè¦å°runä¸çå ç´ ç¿»è½¬ï¼è¿é注æéåºçé¨åå¿ é¡»æ¯âä¸¥æ ¼âéåºæè½è¿è¡ç¿»è½¬ãå 为TimSortçä¸ä¸ªéè¦ç®æ æ¯ä¿æ稳å®æ§ç稳å®æ§ãå¦æå¨è¿ç§æ åµä¸è¿è¡ç¿»è½¬è¿ä¸ªç®æ³å°±ä¸ç¨³å®ï¼ã
1.1è·çæå°é¿åº¦
è¿è¡æ¯å·²ç»æ好åºçä¸åååº.RUNå¯è½ä¼æä¸åçé¿åº¦ï¼Timesortæ ¹æ®è¿è¡çé¿åº¦æ¥éæ©æåºççç¥ãä¾å¦å¦æè¿è¡çé¿åº¦å°äºæä¸ä¸ªå¼ï¼åä¼éæ©æå ¥æåºç®æ³æ¥æåºãè¿è¡çæå°é¿åº¦ï¼minrunï¼åå³äºæ°ç»ç大å°ãå½æ°ç»å ç´ å°äºä¸ªæ¶ï¼é£ä¹è¿è¡çæå°é¿åº¦ä¾¿æ¯æ°ç»çé¿åº¦ï¼è¿æ¯Timsortç¨æå ¥æåºç®æ³æ¥æåºãå½æ°ç»å ç´ å¤§äºçäºæ¶ï¼å¯¹äºè¾å¤§çéµåä¸ï¼ä»å°çèå´å éæ©ä¸ä¸ªç§°ä¸ºminrunçæ°ï¼ä½¿å¾éµåç大å°é¤ä»¥æå°æ¸¸ç¨å¤§å°ï¼çäºæç¥å°äº2çå¹ãæç»çç®æ³åªéè¦æ°ç»å¤§å°ç6个æé«ææä½ï¼å¦æå©ä½çä½è¢«è®¾ç½®ï¼åæ·»å ä¸ä¸ªï¼å¹¶å°è¯¥ç»æç¨ä½minrunã该ç®æ³éç¨äºæææ åµï¼å æ¬æ°ç»å¤§å°å°äºçæ åµã
æ ¹æ® ä¿¡æ¯å¦ç论 ï¼å¨å¹³åæ åµä¸ï¼æ¯è¾æåºä¸ä¼æ¯Oï¼n log nï¼æ´å¿«ãç±äºTimsortç®æ³å©ç¨äºç°å®ä¸å¤§å¤æ°æ°æ®ä¸ä¼æä¸äºæ好åºçåºï¼æ以Timsortä¼æ¯
O对äºéæºæ°æ²¡æå¯ç¨å©ç¨çæ好åºçåºï¼Timsortæ¶é´å¤æ度ä¼æ¯logï¼nï¼ï¼ãä¸è¡¨æ¯Timsortä¸å ¶ä»æ¯è¾æåºç®æ³æ¶é´å¤æ度ï¼time complexityï¼çæ¯è¾ã
第一天:Arrays.sort和Collection实现原理
专栏首秀,坚持写题铸习惯
专栏创建月,笔墨未动。新篇起,android地图导航源码誓成习惯,日日更新,安心之道。
面试题集锦,实则基础学。开发理论,理解为先。
Arrays.sort与Collection.sort揭秘
底层调用,Arrays.sort主导。源码追踪,揭示奥秘。
list.sort与ArrayList实现,继承链,方法调用,逻辑清晰。
Arrays.sort(a, c),比较器调用,逻辑判断,决定排序方式。
LegacyMergeSort.userRequested,关键值,揭示排序策略。
sort(a)调用,进入排序核心。
TimSort的引入,新版本改进,算法优化,效率提升。
总结,TimSort贯穿始终,替代旧有算法,性能更优。
TimSort: C/C++版本
Timsort是一种高效稳定的混合排序算法,融合了优化过的归并排序和二分插入排序。本文将介绍C/C++版本的Tim排序算法,该算法基于Python源码改编,保留了算法的核心部分。读者可参考Python源码和文章了解相关资料。点赞、评论并分享源代码。
TimSort的核心函数包括:1. 数据分块,2. 计算数据块的有序部分,3. 二分插入排序,4. Galloping归并,5. Galloping优化归并,6. 数据块融合顺序。
数据分块
该排序算法采用自底向上的归并排序,无需递归,因此首先需要将数据分割成小块,范围在0-个点之间。根据数据长度计算合适的最小数据块长度,尽量保证数据块数量为2的幂次。
计算每个数据块的有序部分
为了减少不必要的比较和内存拷贝,执行二分排序前,需要计算数据段有序部分的长度。这一步对于重复数据或部分有序数据非常有用,可以减少对象比较和内存拷贝。该函数计算升序和严格降序,降序部分后续会进行翻转。
二分插入排序
对于小规模数据,二分插入排序是最快的。它通过替换正常插入排序的查找部分为二分查找来实现。
Gallop归并
Gallop归并是一种快速查找方式,用于优化两列有序数组的归并过程。通过比较两列数组A,B的最小长度,减少无意义的比较。Gallop模式的核心是,在比较未成功后,加大移动力度,2k+1。这种方法类似于动态数组内存扩展策略,最终比较次数为logn。在发现大致位置后,利用二分查找搜索最终位置。不直接使用二分查找的原因是,其比较次数略高于Gallop。然而,频繁的函数调用会降低性能,因此设定一个阈值,超过阈值时使用Gallop搜索,否则使用正常搜索。
Gallop优化归并
这是算法的精华部分,通过比较法和Gallop来回切换,以达到最佳性能。最小Gallop值决定了是否进入Gallop模式,初始值为7。如果进入次数过多,该值会逐渐增加,以动态适应数据类型。合并两个数组时,左边的数组规模略小于右边。在合并前,先去除已排序的部分。
数据块融合顺序
由于归并采用循环实现,合并顺序对性能有很大影响。理想情况下,相似长度的数据段应先合并。因此,发明者巧妙地使用栈模拟函数递归,通过计算每段数据树的深度来决定是否融合,最后强制融合尾部数据。
主体部分排序大致遵循上述思路
与STL比较,速度提升显著,尤其是在重复数据较多的场景下,TimSort可能接近O(n)复杂度。